经济学10个经典模型之四:
4 囚徒困境(Prisoner’s Dilemma)
安 文
囚徒困境(Prisoner’s Dilemma)是博弈论里面最著名的模型,几乎每本关于博弈论的书籍都会提到。一般人可能不了解博弈论,但很有可能听说过囚徒困境。
故事:两个嫌疑人分别被羁押,警察确定他们违反了某项法律,但并没足够证据治罪。警察告诉两个囚犯,他们有两个选择:承认犯罪行为或拒绝承认。如两个人都拒绝认罪,那么警察将以一些较轻指控立案,如轻微盗窃或非法持有武器,这样两人都将受到较轻处罚(各坐牢1年);如他们都认罪则都会被起诉,但警察将建议法庭从轻处罚(各坐牢5年);如一个人承认而另一个人拒绝认罪,那么认罪的人作为污点证人而受到宽大处理(坐牢0年,无罪释放),另一个人则会受到严厉的处罚(坐牢20年)。
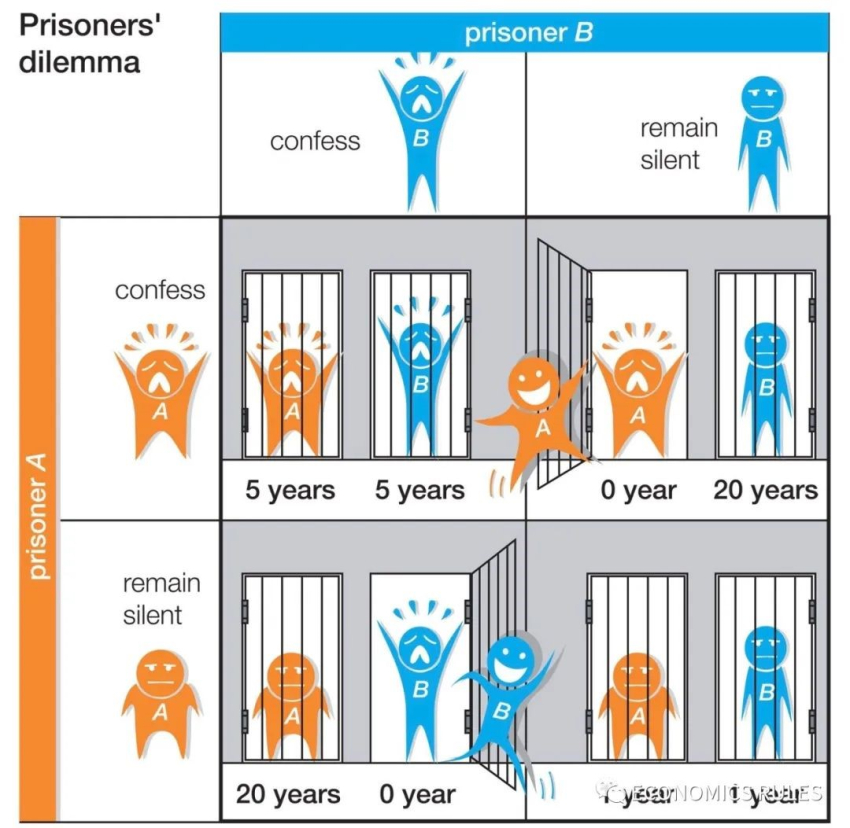
囚徒困境模型的均衡解,是双方都选择承认,非常符合主流经济学个人理性选择、最终获得一个均衡解的模式。但这个均衡解并不是可欲的解,对两囚犯作为一个整体来说,最好结果应该是双方都选择拒绝承认,这样双方各坐牢1年,相比其他结果都要好。但个人理性选择,导致了集体的非理性结果,这就是困境所在。
这个模型也显示了理性经济人与看不见的手带来的乐观和谐之间存在矛盾,引发经济学家们担忧。不过经济学家认为在无限次数或者未知次数博弈的情况下,人们可能会选择合作。
这个模型应用场景非常广泛,在政治学、经济学及生物学等领域都有广泛应用。常见应用场景如军备竞赛、贸易战、广告战、价格战、卡特尔以及公地悲剧等等。
