寻求最佳值与优选的区别

寻求最佳值与优选的区别

葛维亚

       我们做任何事情都力求得到最好的结果。为了达到这一目的，采用优选法或微分方法等两种数学方法最好。然而优选法与微分方法有何不同，到底应该选取哪一个方法，是有讲究的。

       从微积分学得知，对于一个研究系统（对象）可以建立y= f(x)的数学函数关系情况下，当满足一阶导数f`(x)=0，时，或满足一阶微分等于零 ，此时得出的X值对应的y值即为为极值（极大或极小值），可用函数的增减性来判断。可是很多系统无法用的数学函数关系表达，因而只能采用优选法（数学上称为最优化方法）。

       优选法主要是运用一种特殊的数学方法研究各种系统的优化途径及方案，为决策者提供科学决策的依据。 最优化方法的目的在于针对所研究的系统，求得一个合理运用人力、物力和财力的最佳方案，发挥和提高系统的效能及效益。

       最优化方法一般包括变量、约束条件、优选区间、目标函数和精度要求等5要素，采用试算和逐步逼近的方法求得最优值。

1 ,变量：指最优化问题中待确定的某些量。变量可用xn.jpg表示（其中x为变量，n为维数，n=1为1阶变量，n=2为2阶变量，n=3为3阶变量，……. n=n为n阶变量），jpg为静态图片格式。

2，约束条件：指在求最优解时对变量的某些限制，包括技术上的约束、资源上的约束和时间上的约束等。列出的约束条件越接近实际系统，则所求得的系统最优解也就越接近实际最优解。约束条件可用 《=i》=i.jpg，i=1, 2，…，m，m 表示约束条件数;或x∈R(R表示可行集合)。

3，优选区间x：根据实际情况确定x优选范围。

4，目标函数：最优化有一定的评价标准。目标函数就是这种标准的数学描述，一般可用f(x) ) .jpg来表示。目标函数可以是系统功能的函数或费用的函数。它必须在满足规定的约束条件下达到最大或最小。

5，精度要求：根据规范或实际情况确定。

这里以一维变量优选的黄金分割法为例，说明优选计算的方法。

       在一维（即单因素）最优化方法中，黄金分割法（亦称0.618法）是最为流行的一种方法。首先根据问题的实际情况，确定变量及约束条件。而优选区间（  x1,x2.jpg ）作为（0，1）看待，这个优选区间最优值的两个对比点为0.382和0.618。利用已经确定的目标函数公式， 计算着两个对比点的目标函数值，把标函数值不好的那个对比点靠边的那一段去掉， 此时剩下优选的一段长度为第一次优选区间（0，1）长度的0.618倍，用得出的目标函数值进行第二次优选，继而进行第3次，第4次，……….,第n次优选。当第n次优选满足精度要求，即相对误差为δ时（δ根据规范或实际情况决定）， 第n次优选所得到的极值就是最优值。

        其实在优选之前，根据下式，由δ 就可以推求出n值：

             优选精度与优选年数n的关系公式.jpg ：

       

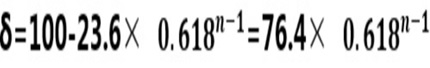
由上式计算可知，优选计算3次，相对精度为91.0%，优选计算5次，相对精度为96.6%。这一方法采用手算，也不费时费力。当然也可以编写电脑程序进行计算。

同时考虑两个或两个以上的变量因子对性能影响规律，这就是多因素优选。

对于多因素优选，首先在直接相互对比中，找出最好的方案，这可以通过简单的比较大小获得。

多因素优选的方法很多，一种为化多为少的方法，其中包括目标法、线性加权法、理想点法等，另一种为分层序列法，除此之外还有单纯形法、爬山法等。在实际应用中，爬山法最为流行，使用者最多。

      

葛维亚，水文水资源博士，科研所总工，教授级高工，著名水文水资源学家，3所著名重点大学特聘教授及博导，我国著名技术期刊审稿人，国务院政府专家津贴获得者。 担任过水利部国家水文数据库专家指导组成员，担任全国多个技术课题鉴定委员会的委员、副主委、主委，亲自起草会议纪要、测试报告以及鉴定评审意见书。 特邀担任全国著名技术刊物审稿者。上世纪七八十年代担任国际水文科学协会IAHS负责人兼驻中国特派员。 退休后，自2006年开始，在网上自建《水文狮子林》个人网站，又在科学网、新浪网、龙城博客网建立博客园地，发表博文九百篇，图片三百多张，全部点击量超过几百万。获得了我国科学网高级会员，金山毒霸钻石会员，博客之星称号。